A car and the stopping force directly proportional to its speed
Task number: 277
A car of the mass m = 1000 kg is going in a straight line at a uniform velocity v0 = 30 m·s-1 on a horizontal road. At a certain time t0 = 0 s a stopping force Fb starts to act against it. The stopping force is directly proportional to the speed of the car. The proportionality constant k = 231 kg·s-1.
1) Find how the speed of the car v(t) and the position of the car x(t) vary with time.
2) Find the time at which the speed is half its initial value, i.e. 15 m·s-1.

Note: Instead of the magnitude of the velocity we further use only the speed.
Hint 1 – The equation of motion
Think about the forces acting on the car and write down the equation of motion for the car.
Hint 2 – the stopping force and the speed v(t)
Express the stopping force Fb from (2) using the speed of the car and solve the resulting differential equation.
Hint 3 - the position of the car x(t)
The dependence of the speed on time is already known. The dependence of the position on time can be obtained by integration.
Hint 4 - the time at which the speed of the car is half its initial value
You are looking for the time when the speed is equal to \(\frac{v_0}{2}\). You know how the speed depends on time.
Complete solution
We draw the acting forces into a figure and write the equation of motion for the car.
The following forces act on the car:
\(\vec{F}_{b}\)...the stopping force
\(\vec{F}_{G}\)...the weight
\(\vec{N}\)...the normal force exerted on the car by the surface
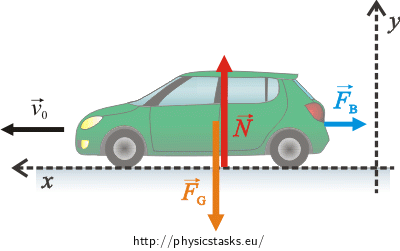
Note: The surface acts on the wheels of the car, we draw its resultant force into the figure.
The equation of motion for the car is:
\[\vec{F}_{b}+\vec{F}_{G}+\vec{N}= m\vec{a}\tag{1}\]
We choose the coordinates following the figure and write the equation (1) in scalar quantities:
\[x:\hspace{20px}-F_b = ma\tag{2}\]
\[y:\hspace{20px}N - F_G = 0\tag{3}\]
Note: The figure explains why there is a minus sign on the left hand side of the equation (2). The stopping force acts against the direction of the car’s motion. The forces \(\vec{F}_{G}\) and \(\vec{N}\) are perpendicular to the stopping force \(\vec{F}_{b}\) They have the same magnitude and opposite directions thus their net force is zero and the acceleration of the car in the direction of the axis y is zero, too.
The expression for the stopping force:
The stopping force Fb is directly proportional to the speed of the car and it can be expressed by the relation:
\[F_{b}=kv\tag{4}\]Inserting it into the equation (2) we obtain:
\[ma=-kv\tag{5}\]We express the acceleration as a change of the speed in time:
\[m\frac{dv}{dt}=-kv\tag{6}\]The speed v(t):
We obtained the first-order differential equation with constant coefficients. We can solve it by a separation of variables.
We rewrite the equation (6) as:
\[\frac{dv}{v}=-\frac{k}{m}dt\]
and integrate both sides of it:
\[ln|v|=-\frac{k}{m}t+C\]
C is a constant of integration.
We take the inverse logarithm of both sides:
\[|v|=e^{-\frac{k}{m}t+C}=e^{-\frac{k}{m}t}\cdot e^{C}\]
The speed is positive thus we do not need to write the symbol of the absolute value. We will denote the constant eC by K.
\[v=K e^{-\frac{k}{m}t }\ \]
We find the value of the constant K from the initial conditions. At the time t = 0 s the speed was equal to v0. Thus:
\[v_0=K e^{-\frac{k}{m}\cdot 0}\ \]
and hence:
\[v_0=K\]
Finally, we get the speed as a function of time:
\[v(t)=v_0\cdot e^{-\frac{k}{m}t}\ \tag{7}\]
We know the dependence of the speed on time.
We obtain the dependence of the position on time by integration:
\[x(t)=\int{v(t)}\,dt\]
\[x(t)=\int{v_0e^{-\frac{k}{m} t}}\,dt\]
\[x(t)=-\frac{mv_0}{k}e^{-\frac{k}{m} t}+C\]
The value of the constant C can be found from the initial conditions. At the time t = 0 s the position of the car was equal to x(0) = 0 m.
Thus:
\[0=-\frac{mv_0}{k}e^{-\frac{k}{m}\cdot 0}+C\]
\[C=\frac{mv_0}{k}\]
The dependence of the car’s position on time is:
\[x(t)=-\frac{mv_0}{k}e^{-\frac{k}{m}\cdot t}+\frac{mv_0}{k}\]
\[x(t)=\frac{mv_0}{k}(1-e^{-\frac{k}{m}t})\tag{8}\]
The time at which the speed of the car is half its initial value:
We insert \(v(t)=\frac{v_0}{2}\) to the expression (7):
\[\frac{v_0}{2}=v_0e^{-\frac{k}{m}t}\ \] \[\frac{1}{2}=e^{-\frac{k}{m}t}\ \]We take the inverse logarithm of both sides:
\[ln\frac{1}{2}=-\frac{k}{m}t\]
\[-\frac{m}{k}ln\frac{1}{2}=t\]
\[\frac{m}{k}ln2=t\tag{9}\]
We insert the numerical values into (9):
\[t=\frac{1000}{231}\cdot 0.693=\frac{693}{231}=3\,\textrm{s}\]
Complete answer
For the dependence of the speed on time it holds \[v(t)=v_0 e^{-\frac{k}{m}t}\] .
For the dependence of the position on time it holds \[x(t)=\frac{mv_0}{k}(1-e^{-\frac{k}{m}t})\] .
The speed of the car is half its original value in 3 s.


