Hiding Place for a Nut
Task number: 1758
Near a tree on which a squirrel lives there is a tunnel that passes through the centre of Earth. The squirrel has decided to hide a nut with mass \(m\) inside the tunnel.

Note: Consider the tunnel to be evacuated (air-less), Earth to be a homogenous sphere and neglect its rotation.
Hint a1)
Use the Newton's law of gravitation to express the gravitational force acting on the nut at a distance \( r\) from the centre of Earth.
Hint a2)
According to equation (5) determine the motion of the nut.
Hint a3)
You know the net force acting on the nut. Write Newton's second law for the nut.
Hint a4)
Solve the differential equation (7). Find its characteristic polynomial and the fundamental system. What were the initial conditions? Find \(r\).
Hint a5)
What is the physical meaning of the term \(\sqrt{\frac{\kappa M}{R^3}}\) in equation (13)?
Hint b)
We now know how the position vector of the nut depends on time. Determine the velocity of the nut using the dependence on time.
Then see how long it will take the nut to get to the centre of Earth and determine the velocity corresponding to this time. Find the numerical solution.
Hint c)
The nut performs harmonic motion, therefore it returns back to the squirrel. The time that it takes corresponds to one period \(T\). Determine it numerically.
Overall solution
a) The motion and the equation of motion of the nut
We formulate Newton's law of gravitation for the force of gravity acting on the nut at a distance r from the centre of Earth.
Let's draw a picture of Earth with a nut where \(R\) is the radius of Earth, \(r\) is the distance of the nut from the Earth's centre, \(m\) is the mass of the nut and \(M_\mathrm{{r}}\) is the mass of Earth that lies inside a sphere of radius \(r\).
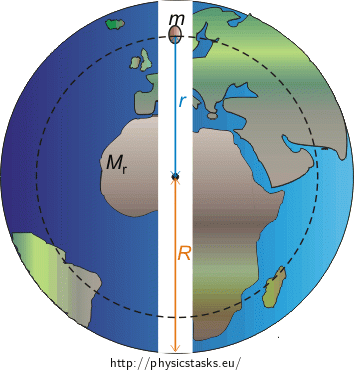
The nut is acted on by the force of gravity, which is caused by the part of Earth with mass \(M_\mathrm{{r}}\), the net force of the rest of Earth is zero .
We write the equation for \(M_{\mathrm{r}}\): \[M_{\mathrm{r}}=\rho V_{\mathrm{r}},\tag{1}\] where \(\rho\) is the density of homogeneous Earth and \(V_{\mathrm{r}}\) is the volume which is enclosed by the dashed line in the picture above. The volume \(V_{r}\) can be written as: \[V_{\mathrm{r}}=\frac{4\pi r^3}{3}.\tag{2}\] Now we substitute equation (2) in equation (1): \[M_{\mathrm{r}}=\rho \frac{4\pi r^3}{3}.\tag{3}\]
The gravitational force acting on the nut at a distance \(r\) from the centre of Earth is as follows \[F=-\kappa \frac{mM_{r}}{r^2},\tag{4}\] where \(\kappa\) is the gravitational constant. We substitute equation (3) into equation (4): \[F=-\kappa \frac{m\rho \frac{4\pi r^3}{3}}{r^2}.\] We divide the fraction by \(r^2\) and adjust it: \[F=-\kappa \frac{m\rho 4\pi r}{3}.\tag{5}\]
The motion of the nut
We denote the constants in the equation (5) by \(k=\kappa \frac{m\rho 4\pi }{3}\): \[F=-kr.\] This relationship is similar to the relationship for the tensile force in Hook's law (case of tensile/pressure strain). The nut behaves like a harmonic oscillator and performs a harmonic motion
Newton's second law
We express Newton's second law for the force acting on the nut: \[F=ma,\] where \(a\) is the acceleration of the nut.
We write the acceleration as the second derivative of distance \(r\) of the nut from the centre of Earth with respect to time \(t\): \[F=m \frac{\mathrm{d}^2r}{\mathrm{d}t^2}.\tag{6}\]
Now we substitute from equation (5): \[-\kappa \frac{m\rho 4\pi r}{3}=m \frac{\mathrm{d}^2r}{\mathrm{d}t^2}.\] We divide both sides of the equation by \(m\) and multiply the left side of the equation by number one in the form of \(\frac{R^3}{R^3}\): \[-\kappa \frac{\rho 4\pi r}{3}\frac{R^3}{R^3}= \frac{\mathrm{d}^2r}{\mathrm{d}t^2}.\] \(\frac{\rho 4\pi}{3}{R^3}\) is the mass \(M \) of Earth and therefore: \[-\kappa \frac{Mr}{R^3}= \frac{\mathrm{d}^2r}{\mathrm{d}t^2}.\] Now we move both members of the equation to one side of the equation: \[ \frac{\mathrm{d}^2r}{\mathrm{d}t^2}+\frac{\kappa M}{R^3}r=0.\tag{7}\]
The solution of differencial equation (7)
Determine the characteristic polynomial of equation (7): \[ \lambda^2+\frac{\kappa M}{R^3}\lambda^0.\] We want to determine the roots of this polynomial, so we write the polynomial equation: \[ \lambda^2+\frac{\kappa M}{R^3}\lambda^0=0.\] We realize that \(\lambda^0=1\) and then we subtract the member \(\frac{\kappa M}{R^3}{\cdot}1\) from both sides of the equation: \[ \lambda^2=-1\frac{\kappa M}{R^3}.\] In order make the square root of both sides of the equation, we must first write \(-1\) on the right side as the square of imaginary unit \(i^2\): \[ \lambda^2=i^2\frac{\kappa M}{R^3}.\] Now we can make the square root of both sides: \[ \lambda = ± i\sqrt{\frac{\kappa M}{R^3}}.\] The roots of characteristic polynomial are \(i\sqrt{\frac{\kappa M}{R^3}}\) a \(-i\sqrt{\frac{\kappa M}{R^3}}\).
The fundamental system therefore is \(e^{i\sqrt{\frac{\kappa M}{R^3}}t}\) a \(e^{-i\sqrt{\frac{\kappa M}{R^3}}t}\).
The solution of equation (7) is in the form of: \[r=Ae^{i\sqrt{\frac{\kappa M}{R^3}}t}+Be^{-i\sqrt{\frac{\kappa M}{R^3}}t}.\tag{8}\]
To determine the constants \(A\) and \(B\) we need to apply the initial conditions.
The moment the squirrel dropped the nut into the tunnel was at time zero \(t=0\), the distance of the nut from the centre of Earth was equal to the radius of Earth \(r=R\) and the velocity of the nut was zero \(v = \frac{\mathrm{d}r}{\mathrm{d}t}=0\).
We substitute the initial conditions \(t=0\) and \(r=R\) into the relationship (8): \[R=Ae^{i\sqrt{\frac{\kappa M}{R^3}}0}+Be^{-i\sqrt{\frac{\kappa M}{R^3}}0}.\] Since \(e^0=1\), then: \[R=A+B.\tag{9}\]
We derive the relationship (8) with respect to time: \[\frac{\mathrm{d}r}{\mathrm{d}t}=i\sqrt{\frac{\kappa M}{R^3}}Ae^{i\sqrt{\frac{\kappa M}{R^3}}t}-i\sqrt{\frac{\kappa M}{R^3}}Be^{-i\sqrt{\frac{\kappa M}{R^3}}t}.\] Now we substitute \(t=0\) and \(\frac{\mathrm{d}r}{\mathrm{d}t}=0\): \[0=i\sqrt{\frac{\kappa M}{R^3}}Ae^0-i\sqrt{\frac{\kappa M}{R^3}}Be^0.\] \(e^0\) is equal to \(1\) and we divide both sides of the equation by \(i\sqrt{\frac{\kappa M}{R^3}}\): \[0=A-B.\] We add \(B\) to both sides of the equation: \[A=B.\tag{10}\] Substituting the relation (10) into (9): \[R=B+B=2B.\] We divide both sides two and evaluate \(B\): \[B=\frac{R}{2}.\] According to (10) it applies: \[A=B=\frac{R}{2}.\tag{11}\] We substitute (11) do (8): \[r=\frac{R}{2}e^{i\sqrt{\frac{\kappa M}{R^3}}t}+\frac{R}{2}e^{-i\sqrt{\frac{\kappa M}{R^3}}t}.\tag{12}\]
Furthermore it is true that \(e^{iα}=\cos{α}+i\sin{α}\) and \(e^{-iα}=\cos{α}-i\sin{α}\). Equation (12) can then be rewritten as: \[r=\frac{R}{2}\cos{\sqrt{\frac{\kappa M}{R^3}}t}+i\frac{R}{2}\sin{\sqrt{\frac{\kappa M}{R^3}}t}+\frac{R}{2}\cos{\sqrt{\frac{\kappa M}{R^3}}t}-i\frac{R}{2}\sin{\sqrt{\frac{\kappa M}{R^3}}t}.\] We add the members with sine and cosine together: \[r=R\cos{\sqrt{\frac{\kappa M}{R^3}}t}.\tag{13}\]
The physical meaning of the term \(\sqrt{\frac{\kappa M}{R^3}}\) in equation (13)
Since the nut performs harmonic motion, the term is its angular frequency \( ω\): \[ω=\sqrt{\frac{\kappa M}{R^3}}.\tag{14}\] Relationship (13) can therefore be rewritten as: \[r=R\cos{ωt}.\]
b) The velocity of the nut passing through the centre of Earth
The dependence of the velocity of the nut on the time can be found by deriving the position vector.
We derivate equation (13): \[\begin{eqnarray}\frac{\mathrm{d}r}{\mathrm{d}t} &= &\frac{\mathrm{d}}{\mathrm{d}t}\left(R\cos{\sqrt{\frac{\kappa M}{R^3}}t}\right),\\ v &= &-R\sqrt{\frac{\kappa M}{R^3}}\sin{\sqrt{\frac{\kappa M}{R^3}}t}.\\ \end{eqnarray}\]
It takes the nut one quater of its period \(T\) to reach the centre of Earth: \[t=\frac{1}{4}T.\] Period is given by the relation \(T=\frac{2 \pi}{ω}\), in which we substitute ω from equation (14): \[T=2 \pi \sqrt{\frac{R^3}{\kappa M}}.\tag{15}\] For time \(t\) it applies: \[t=\frac{1}{4}T=\frac{1}{4}2 \pi \sqrt{\frac{R^3}{\kappa M}}=\frac{\pi}{2}\sqrt{\frac{R^3}{\kappa M}}.\]
We substitute \(t\) in the relation for velocity and adjust the equation (\({\sqrt{\frac{\kappa M}{R^3}}\sqrt{\frac{R^3}{\kappa M}}}=1\), \(\sin{\frac{\pi}{2}}=1\), \(\frac{R^2}{R^3}=\frac{1}{R}\)): \[v=-R\sqrt{\frac{\kappa M}{R^3}}\sin{\sqrt{\frac{\kappa M}{R^3}}\frac{\pi}{2}\sqrt{\frac{R^3}{\kappa M}}}=-\sqrt{\frac{\kappa MR^2}{R^3}}\sin{\frac{\pi}{2}}=-\sqrt{\frac{\kappa M}{R}}. \] The velocity of the nut passing through the centre of Earth is equal to: \[v = \sqrt{\frac{\kappa M}{R}}.\] We look up the values for \(R\), \(M\) and \(\kappa\) in the Handbook of Chemistry and Physics:
radius of Earth \(R \dot =6{,}378\cdot{10}^3 \mathrm{m}\) mass of Earth \(M \dot= 5{.}97\cdot{10}^{24} \mathrm{kg}\) gravitational constant \(\kappa \dot= 6{.}67\cdot{10}^{-11} \mathrm{\frac{m^3}{kg\cdot s^{2}}}\) We determine the velocity numerically: \[v = \sqrt{\frac{6{.}67\cdot{10}^{-11}\cdot 5{.}97\cdot{10}^{24}}{6{,}378\cdot{10}^3} \mathrm{\frac{\frac{m^3}{kg\cdot s^{2}}\cdot kg}{m}}} \dot= 7{,}900 \mathrm{\frac{m}{s}} \dot= 28{,}440 \mathrm{\frac{km}{h}}.\]
c) When the nut returns
The nut performs harmonic motion, therefore it returns back to the squirrel. The time that it takes corresponds to one period \(T\).
We use relationship (15) we determined for the period: \[T=2 \pi \sqrt{\frac{R^3}{\kappa M}}.\] We look up the values for \(R\), \(\kappa\), \(M\) and \(\pi\) in The Handbook of Chemistry and Physics:
The nut returns back to the squirrel in time: \[T=2 {\cdot}3{.}14 \sqrt{\frac{\left(6378{\cdot} 10^3\right) ^3}{6{.}67\cdot{10}^{-11}\cdot 5{.}97\cdot{10}^{24}} \frac{\mathrm{m^3}}{\mathrm{\frac{m^3}{kg\cdot s^2}}\mathrm{kg}}} \dot= 5{,}069 \mathrm{s} \dot= 84 \mathrm{min},\] \[T \dot= 1 \mathrm{h} 24 \mathrm{min}.\]radius of Earth \(R \dot= 6{,}378\cdot{10}^3 \mathrm{m}\) gravitational constant \(\kappa \dot= 6{.}67\cdot{10}^{-11} \mathrm{\frac{m^3}{kg\cdot s^2}}\) mass of Earth \(M \dot= 5{.}97\cdot{10}^{24} \mathrm{kg}\) Ludolf's number \(\pi \dot= 3{.}14\) Answer
a) The nut performs harmonic motion. The equation of its motion is \( \frac{d^2r}{dt^2}+\frac{\kappa M}{R^3}r=0\). And \(r=R\cos{ωt}\), where \(ω=\sqrt{\frac{\kappa M}{R^3}}\).
b) The velocity of the nut when passing through the centre of Earth is equal to \(v=-\sqrt{\frac{\kappa M}{R}} \), numerically \(v \dot= 28 440 \mathrm{\frac {km}{h}}. \)
c) The nut returns to the squirrel in time \(T=2 \pi \sqrt{\frac{R^3}{\kappa M}}\), therefore approximately in one hour and twenty four minutes.


