Weight on rope
Task number: 1521
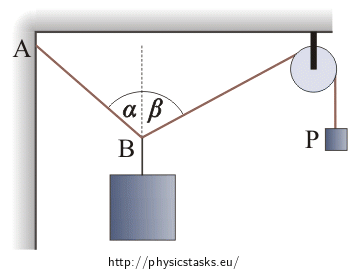
Notation
mb = 10 kg mass of weight B α = 45° desired angle between rope AB and the vertical line β = 60° desired angle between the rope from B to the pulley and the vertical line mp =? (kg) mass of weight P Fa =? (N) stress of rope AB Hint 1
Draw all the forces acting on the weights B and P in the figure. What must be valid for their resultant?Hint 2
Choose an appropriate coordinate system and rewrite the equations (1) and (2) as a scalar. Express the searched parameters from the obtained equations.
Solution
We draw all the forces acting on the weights B and P to the figure and choose the coordinate system.
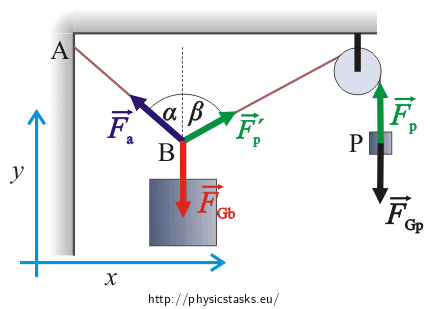
Weight P:
\(\vec{F}_{Gp}\) .......weight force (FGp = mpg)
\(\vec{F}_{p}\).......force, by which the rope is pulled
Weight B:
-
\(\vec{F}_{Gb}\) .......weight force (FGb = mbg)
-
\(\vec{F^,}_{p}\) ....... force, which the rope with the weight P is pulled by
(The pulley is at standstill so that it is valid for the values of forces \(\vec{F}_{p}\) and \(\vec{F^,}_{p}\) that Fp = F´p, The weight P pulls the rope with the weight B and vice versa)
-
\(\vec{F}_{a}\) ....... force, by which the rope mounted to the wall is pulled
Both weights are at standstill so the resultant of acting forces must be equal to the zero vector.
Weight P:
\[\vec{F}_{Gp}+\vec{F}_{p}=\vec{0}\,.\tag{1}\]Weight B:
\[\vec{F}_{Gb}+\vec{F'}_{p}+\vec{F}_{a}=\vec{0}\,.\tag{2}\]We rewrite the equations (1) and (2) as a scalar:
Weight P:
\[{F}_{p}=F_{Gp}=m_pg\,.\]
Weight B:
\[x:\hspace{60px}F_p\sin\beta-F_a\sin\alpha=0\tag{3}\]
\[y:\hspace{10px}F_a\cos\alpha+F_p\cos\beta-F_{Gb}=0\tag{4}\]
From equation (3):
\[F_a = F_p \frac{\sin \beta}{\sin \alpha}\,.\tag{5}\]We substitute into the equation (4):
\[F_p \frac{\sin \beta}{\sin \alpha} \cos \alpha + F_p \cos \beta = F_{Gb}\,.\]And modify:
\[F_p\frac{\sin\beta\cos\alpha+\sin\alpha\cos \beta}{\sin \alpha} = F_{Gb}\,.\]Using the addition formula for sine:
\[F_p\sin(\alpha+\beta)=F_{Gb}\sin\alpha\,,\] \[F_p=F_{Gb}\frac{\sin\alpha}{\sin(\alpha+\beta)}\,.\]So:
\[gm_p=gm_b\frac{\sin\alpha}{\sin(\alpha+\beta)}\,,\] \[m_p=m_b\frac{\sin\alpha}{\sin(\alpha+\beta)}\,.\]We substitute gained Fp to the equation (5):
\[F_a = F_{Gb} \frac{\sin \alpha}{\sin (\alpha + \beta)} \frac{\sin \beta}{\sin \alpha}\,,\] \[F_a = F_{Gb} \frac{\sin \beta}{\sin (\alpha + \beta)}\,,\] \[F_a = gm_{b} \frac{\sin \beta}{\sin (\alpha + \beta)}\,.\]We substitute given values:
α, β, mb:
\[m_p=10\frac {\sin45^\circ}{\sin(45^\circ+60^\circ)}\,\mathrm{kg}\dot{=}7{,}3 \,\mathrm{kg}\,,\] \[F_a=10{\cdot}10\frac {\sin60^\circ}{\sin(45^\circ+60^\circ)}\,\mathrm{N} \dot{=} 90 \,\mathrm{N}\,.\]Answer
Demanded mass of weight P is equal to:
\[m_p=m_b\frac{\sin\alpha}{\sin(\alpha+\beta)}\,.\]The stress in rope AB is equal to:
\[F_a = gm_{b} \frac{\sin \beta}{\sin (\alpha + \beta)} \,.\]Numerically:
\[m_p \dot{=}7.3 \,\mathrm{kg}\,,\] \[F_a \dot{=} 90 \,\mathrm{N}\,.\]