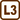Scissors and suspended rod
Task number: 1516
The rod with length of \(3l\), and insignificant mass is suspended in horizontal position using two fibers attached to ends of the rod. There are balls with masses of \(m\) and \(2m\) fixed to the rod, so their centers are placed in one third or two thirds of the rod‘s length. Balls‘ radiuses are very small compared to rod’s length.
Calculate, how the force straining the fiber on the smaller ball’s side is changed when we cut the second fiber.
Preparatory guide
The rigid body can be with advantage replaced with system of mass points in some cases during solving problems. We’ll use it in this task.Impulse theorem
The resultant force of external forces acting on system mass points is equal temporal change of total momentum of the system. The second equation is valid in the same time and is generalization of the Newton’s law of force on the system of mass points, where \(\vec{a_\mathrm{T}}\) is acceleration of center of gravity and \(m\) is mass of system.
\[\sum_{i=1}^{N}\vec{F}_i = \frac{\mathrm{d}\vec{p}}{\mathrm{d}t}= m\vec{a}_\mathrm{T}. \] If there’s acceleration of the system null (is at rest or move lineary with constant velocity) \[\sum_{i=1}^{N}\vec{F}_i = \vec{0}.\]Angular momentum theorem
Angular momentum theorem says, that temporal change of angular momentum of the system equals resultant moment of external forces acting on system. The second equation is valid in case of rotation around fixed axis, where \(J\) is moment of inertia around the axis and \(\vec{\varepsilon}\) is angular acceleration. \[\sum_{i=1}^{N}\vec{M}_i = \frac{\mathrm{d}\vec{L}}{\mathrm{d}t}= J\vec{\varepsilon}. \]Relation between angular and peripheral quantities
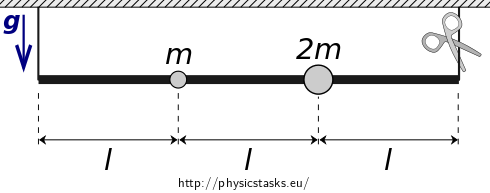
Point \(\mathrm{T}\) is rotating around point \(\mathrm{O}\) so \(|\mathrm{OT}| = \mathrm{konst.}\)
His positions in time \(t\) and \(t + \mathrm{d}t\) are plotted in following figure.
Elementary shift \(\mathrm{d}s\) on the arc of the circle with radius \(r = |\mathrm{OT}|\) after turn by elementary angle \(\mathrm{d}\varphi\) (in radians!) is
\[\mathrm{d}s = r \mathrm{d} \varphi.\] If we’re interested in acceleration of that movement, which is the second derivative of track with respect to time, we can obtain by using sequential modifications from previous equation \[a = \frac{\mathrm{d}^2 s}{\mathrm{d}t^2} = \frac{\mathrm{d}}{\mathrm{d}t}\left( \frac{\mathrm{d}s}{\mathrm{d}t}\right) = \frac{\mathrm{d}}{\mathrm{d}t}\left( \frac{r\mathrm{d}\varphi}{\mathrm{d}t}\right) = r\frac{\mathrm{d}}{\mathrm{d}t}\left( \frac{\mathrm{d}\varphi}{\mathrm{d}t}\right) = r \frac{\mathrm{d}^2 \varphi}{\mathrm{d}t^2} = r\varepsilon,\] i.e. link between peripheral acceleration on the left and angular acceleration on the right side of the equation.Note: Notice that radius \(r\) is factored out derivative during modifications. This edit is only possible if \(r\) is constant. Position of the center of gravity relative to the axis of rotation is constant in this task so we can use this equation.
Calculation of position of the center of gravity
If mass points \(m_i\) are in line and \(x_i\) are their coordinates to the point \(\mathrm{O}\), coordinate of the center of gravity is \[x_\mathrm{T} = \frac{\sum_{i=1}^N m_i x_i}{\sum_{i=1}^N m_i}.\]Moment of inertia
Moment of inertia is additive quantity. For system of mass points \(m_i\) with distance from axis of rotation \(\vec{r}_i\) the moment of inertia around the axis is \[J = \sum_{i=1}^N m_i r_i^2.\]Notation
\(m, 2m\) mass of the balls \(l\) distance of the balls
\(\tilde T_1^\prime/ \tilde T_1 = \mathrm{?}\) ratio of the strength on fiber after to strength before cut the second fiber Hint 1 - force before cut
Draw all forces affect rod with balls into the picture. Rod with balls is at rest before cut – resultant vectors of external forces and their torques are zero.
Write equations expressing balance conditions and express the force which left fiber affects the rod with.Hint 2 - force after cut
System of rod and balls will start rotating about the point \(\mathrm{O}\) after right fiber is cut.
Draw all external forces affect the system. Then lay out the theorems for this system, i.e. express right side of the equations
\[M\vec{a_\mathrm{T}} = \sum_{i=1}^N \vec{F_i}, \qquad J\vec{\varepsilon} = \sum_{i=1}^N \vec{M_i},\]and transcribe them into scalar form.
Hint 3 - force after cut
- Determine moment of inertia \(J\) of the system around the axis, if we regard balls as mass points considering their small radius.
- Realize how acceleration of center of gravity \(a_\mathrm{t}\) depends on angular acceleration \(\varepsilon\).
- Express coordinate of the center of gravity to point O.
Find magnitude of force \(T_1^\prime\), which the left fiber affects the rod just after cutting the right fiber with.
Hint 4 - change of force in the cut moment
We’ve got expressed forces \(T_1\) and \(T_1'\) affecting the rod before and after cut the fiber.
What are magnitudes of forces \(\tilde T_1\) and \(\tilde T_1'\) straining the fiber at the same time? How the force straining left fiber changes after cut right fiber?
COMPLETE SOLUTION
We draw all external forces affect the rod.- gravity forces \(\vec{F_{\mathrm{G1}}}\), \(\vec{F_{\mathrm{G2}}}\)of balls with mass \(m\) and \(2m\),
- tensile forces \(\vec{T_1}\) and \(\vec{T_2}\)rod on fibers,
- gravity force of the rod is zero, because we disregard its mass.
Rod with balls is at rest; resultant vectors of external forces and their moments are zero i.e. \[ \vec{F_{\mathrm{G1}}} + \vec{F_{\mathrm{G2}}} + \vec{T_1} + \vec{T_2} = \vec{0}, \] \[ \vec{l}\times\vec{F_{\mathrm{G1}}} + 2\vec{l}\times\vec{F_{\mathrm{G2}}} + \vec{0} \times \vec{T_1} + 3\vec{l}\times\vec{T_2} = \vec{0}, \] where moments are around left end of the rod, i.e. point \(\mathrm{O}\).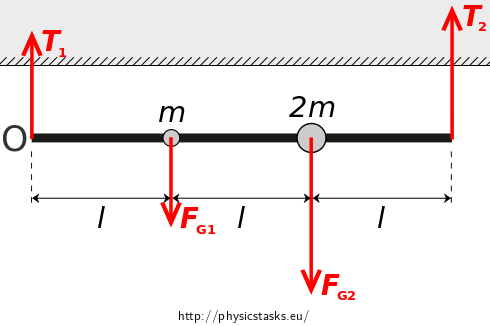
We transcribe equation in scalar form
\[ {F_{\mathrm{G1}}} + {F_{\mathrm{G2}}} - {T_1} - {T_2} = 0, \] \[ -{lF_{\mathrm{G1}}} - 2l{F_{\mathrm{G2}}} + 3l{T_2} = 0, \] where the magnitudes of torques with orientation in front of the picture plane are positive and with orientation behind the picture plane are negative.Substituting for gravity forces we gain equations
\[ mg + 2mg - {T_1} - {T_2} = 0, \tag{1}\] \[ -lmg - 4lmg + 3l{T_2} = 0. \tag{2}\]We divide the second equation by l and modify
\[3{T_2} = 5mg\] \[T_2 = \frac{5}{3}mg\]We express unknown \(T_1\) from equation (1) and substitute for \(T_2\) into it.
\[T_1 = 3mg - T_2\] \[ T_1 = 3mg - \frac{5mg}{3} = \frac{4}{3}mg. \tag{A}\]
We draw all external forces affect the system after right fiber is cut into the picture.- gravity forces \(\vec{F_{\mathrm{G1}}}\), \(\vec{F_{\mathrm{G2}}}\) of balls do not change,
- tensile force \(\vec{T_2}\) stops affecting when fiber is cut ,
- tensile force \(\vec{T_1}\) transforms into force \(\vec{T_1^\prime}\),
- gravity force of the rod is still zero, because we disregard its mass.
Rod starts rotating around the point \(\mathrm{O}\).
According to the theorems we form equations of motion \[ \vec{F_{\mathrm{G1}}} + \vec{F_{\mathrm{G2}}} + \vec{T_1^\prime} = M\vec{a_\mathrm{T}}, \] \[ \vec{l}\times\vec{F_{\mathrm{G1}}} + 2\vec{l}\times\vec{F_{\mathrm{G2}}} + \vec{0} \times \vec{T_1^\prime} = J\vec{\varepsilon}, \] where \(M\) is mass of the system, \(J\) moment of inertia around the axis and \(\varepsilon\) is angular acceleration. The moments are around the left end of the rod again, i.e. point \(\mathrm{O}\).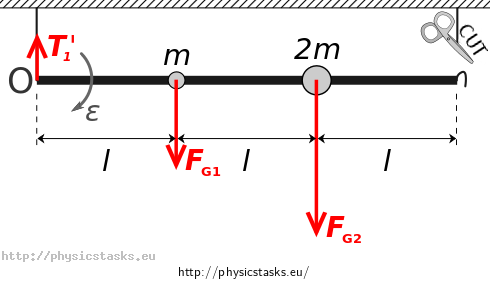
We transcribe equations into scalar form
\[ {F_{\mathrm{G1}}} + {F_{\mathrm{G2}}} - {T_1^\prime} = Ma_\mathrm{T}, \] \[ -{lF_{\mathrm{G1}}} - 2l{F_{\mathrm{G2}}} = -J\varepsilon, \] where the magnitudes of moments with orientation in front of the picture plane are positive and with orientation behind the picture plane are negative.Substituting for gravity forces and mass of the system \(M = 3m\) we gain equations
\[ 3mg - T_1^\prime = 3m a_\mathrm{T}, \tag{3}\] \[ 5lmg = J\varepsilon. \tag{4}\] Moment of inertia \(J\) of the system around the axis trough point \(\mathrm{O}\) with balls replaced with mass points is \[ J = ml^2 + 2m(2l)^2 = 9ml^2. \tag{5}\] Balls are fixed to the rod. Center of gravity is unchanging just as axis. So distance the center of gravity and axis is constant and the acceleration of the center of gravity \(a_\mathrm{T}\) is bound by this radius of the rotation to the angular acceleration \(\varepsilon\) with the term \[a_\mathrm{T}=r_\mathrm{T} \varepsilon.\tag{6}\]Radius of the rotation of the center of gravity \(r_\mathrm{T}\) is the coordinate of the center of gravity to point \(\mathrm{O}\), i.e.
\[r_\mathrm{T} = \frac{ml + 2m2l}{m+2m} = \frac{5}{3}l.\tag{7}\]We substitute into equation (3) \(a_\mathrm{T}\) from (6),in which we substituted \(r_\mathrm{T}\) from (7). We substitute into equation (4) \(J\) from (5).
\[3mg-T_1^\prime = 3m \frac{5}{3} l \varepsilon,\tag{8}\] \[5lmg = 9ml^2\varepsilon.\tag{9}\] We divide equation (8) by (9), so we eliminate \(\varepsilon\) and express unknown \(T_1^\prime\). \[ \frac{3mg-T_1^\prime}{5lmg} = \frac{5}{9l} \] \[ \Longrightarrow T_1^\prime = \frac{2}{9}mg. \tag{B}\]
Left fiber affects left end of the rod with the force \(T_1\) (or \(T_1^\prime\)), end of the rod affects the same fiber with the force \(\tilde T_1\) (or \(\tilde T_1^\prime\)), which straining the fiber. From the law of action and reaction holds \[T_1 = \tilde T_1 \qquad a \qquad T_1 = \tilde T_1^\prime.\] Forces straining the fiber are in ratio \[\frac{\tilde T_1^\prime}{\tilde T_1} = \frac{T_1^\prime}{T_1} = \frac{\frac{2}{9}mg}{\frac{4}{3}mg} = \frac{1}{6},\] where we used results (A) and (B).Answer
The force straining the fiber at left end of the rod decreases six times at the moment of cut.