Motion Given by a Motion Graph III
Task number: 1748
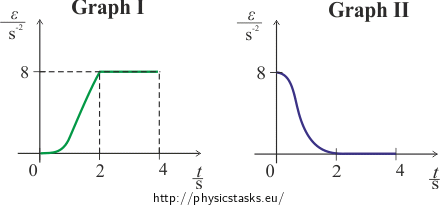
The time dependence of the angular acceleration ε of a spinning circular disk is shown in the graphs I and II. There is a point A marked at the edge of the disk. Determine analytically the time dependence of angular acceleration ε(t), angular speed ω(t), and angular deviation α(t) over the interval <0; 4 s>.
The point A at time t = 0 s is at rest and the angular deviation of the point is zero.
Graph I is partly a parabola and partly a line. Graph II is composed of a sine wave and a line.
Note: The parametric equations should be in the form:
\[y (t) \,=\, 1\,\mathrm{m}-2\,\mathrm{m\cdot s^{-1} }\cdot t.\]We won’t write the units to make the notation simpler.
Hint 1 for graph I: Time dependence of ε(t)
Divide the graph into two intervals.
What functions can be used to represent the graph of ε(t)?
Write the equations of these functions. You need at least two points of the graph with known coordinates to do that. Which points can you use?
Hint 2 for graph I: Time dependence of ω(t) and α(t)
You know the time dependence of ε(t). How can you use it to determine the time dependence of angular speed ω(t)? The process is analogous to the one used in the case of a linear motion.
When you know the time dependence of angular speed, you can use a similar process as before to determine the time dependence of angular deviation α(t).
Hint 3 for graph II: Time dependence of ε(t)
Proceed as with graph I. Divide the graph of ε(t) into two intervals.
What functions can be used to represent the graph of ε(t)?
Write the equations of these functions.
Hint 4 for Graph II: Time dependence of ω(t) and α(t)
You know the time dependence of the angular acceleration ε(t). How can you use it to determine the time dependence of the angular speed ω(t)? The process is analogous to the one used in the case of a linear motion.
When you know the time dependence of angular speed, you can use a similar process as before to determine the time dependence of angular deviation α(t).
The process is the same as with graph I.
COMPLETE SOLUTION
We will divide the graph of ε(t) into two intervals,
interval <0 s; 2 s> and interval (2 s; 4 s>.
Graph I, interval <0 s; 2 s>:
The graph of the function ε(t) over this interval is \(\varepsilon (t) = at^{2}\)
(a parabola that intersects the origin).
The point [2; 8] lies on the parabola, therefore:
\[8\,=\,a2^{2},\] \[a\,=\,2.\]The equation for \(\varepsilon(t)\) is then:
\[\varepsilon(t) \,=\, 2t^{2}.\]We know the equation of the function \(\varepsilon(t)\). We also know that for \(\omega(t)\) it holds that:
\[\omega(t)\,=\,\int{\varepsilon(t)}dt.\]Therefore:
\[\omega(t)\,=\, \int{2t^{2}}dt \,=\, 2\frac{t^{3}}{3}\,+\,C.\]We will determine the constant of integration C from the initial conditions:
\[t\,=\,0\,\mathrm{s}, \hspace{20px} \omega(0)\,=\,0,\] \[0\,=\,0\,+\,C,\] \[C\,=\,0,\]
\[\omega(t)\,=\,\frac{2}{3}t^3.\]For \(\alpha(t)\) we get:
\[\alpha(t)\,=\,\int{\omega(t)}dt,\] \[\alpha(t)\,=\,\int{\frac{2}{3}t^3}dt \,=\, \frac{2}{3}\,\frac{t^{4}}{4}\,+\,C.\]We will determine the constant of integration C from the initial conditions:
\[t\,=\,0\,\mathrm{s}, \hspace{20px} \alpha(0)\,=\,0,\] \[0\,=\,0\,+\,C,\] \[C\,=\,0,\]
\[\alpha(t)\,=\,\frac{t^{4}}{6}.\]Graph I, interval (2 s; 4 s>:
The graph of the function ε(t) over this interval is: \(\varepsilon(t)\,=\,8.\)
We also know that for \(\omega(t)\) it holds that:
\[\omega(t)\,=\,\int{\varepsilon(t)}dt,\] \[\omega(t)\,=\,\int{8}dt\,=\, 8t\,+\,C.\]We know the equation for \(\omega(t)\) over the interval <0 s; 2 s>, so we can calculate the value of \(\omega(2)\) at time 2 s:
\[\omega(2)\,=\,\frac{2}{3}\cdot2^{3}\,=\,\frac{16}{3}.\]We can calculate the constant C:
\[t\,=\,2\,\mathrm{s}, \hspace{20px} \omega(2)\,=\,\frac{16}{3},\] \[\frac{16}{3}\,=\,8{\cdot}2\,+\,C,\] \[C\,=\,-\frac{32}{3},\]
\[\omega(t)\,=\,8t\,-\,\frac{32}{3}.\]We will use the same procedure to get \(\alpha(t)\):
\[\alpha(t)\,=\,\int{\omega(t)}dt,\] \[\alpha(t)\,=\, \int({8t\,-\,\frac{32}{3}})dt \,=\, 4t^{2}\,-\,\frac{32}{3}t\,+\,C.\]We know the equation for \(\alpha(t)\) over the interval <0 s; 2 s>, so we can calculate the value of \(\alpha(2)\) at time 2 s:
\[\alpha(2)\,=\,\frac{2^4}{6}\,=\,\frac{16}{6}\,=\,\frac{8}{3}.\]We can calculate the constant C:
\[t\,=\,2\,\mathrm{s}, \hspace{20px} \alpha(2)\,=\,\frac{8}{3},\] \[\frac{8}{3}\,=\,4{\cdot}2^{2}\,-\,\frac{32}{3}\cdot2\,+\,C,\] \[C\,=\,8,\]
\[\alpha(t)\,=\,4t^{2}\,-\,\frac{32}{3}t\,+\,8.\]Graph II, interval <0 s; 2 s>:
We proceed as with graph I.
The graph of the function ε(t) over this interval is a cosine function. The general form of a cosine function is:
\[\epsilon(t)\,=\,A\cos\frac{2\pi}{T}(t\,-\,C)\,+\,D,\]Where A is the amplitude, T is the period, C is the horizontal shift and D is the vertical shift.
In our case: A = 4 s−2, T = 4 s, C = 0, D = 4 s−2, and therefore:
\[\epsilon(t)\,=\,4\cos\frac{\pi}{2}t\,+\,4.\]We know the equation of the function \(\epsilon(t)\). We also know that for \(\omega(t)\) it holds that:
\[\omega(t)\,=\,\int{\epsilon(t)}dt,\] \[\omega(t)\,=\, \int{(4\cos\frac{\pi}{2}t\,+\,4)}dt \,=\, \frac{8}{\pi}\sin\frac{\pi}{2}t\,+\,4t\,+\,C.\]We will determine the constant of integration C from the initial conditions:
\[t\,=\,0\,\mathrm{s}, \hspace{20px} \omega(0)\,=\,0,\] \[0\,=\,\frac{8}{\pi}\sin0\,+\,0\,+\,C,\] \[C\,=\,0,\]
\[\omega(t)\,=\,\frac{8}{\pi}\sin\frac{\pi}{2}t\,+\,4t.\]For \(\alpha(t)\) we get:
\[\alpha(t)\,=\,\int{\omega(t)}dt,\] \[\alpha(t)\,=\,\int{(\frac{8}{\pi}\sin\frac{\pi}{2}t\,+\,4t)}dt \,=\, -\frac{16}{\pi^{2} }\cos\frac{\pi}{2}t\,+\,2t^{2}+C.\]We will determine the constant of integration C :
\[t\,=\,0\,\mathrm{s}, \hspace{20px} \alpha(0)\,=\,0,\] \[0\,=\,-\frac{16}{\pi^{2} }\cos0\,+\,0\,+\,C,\] \[C\,=\,\frac{16}{\pi^{2} },\]
\[\alpha(t)\,=\,-\frac{16}{\pi^{2} }\cos\frac{\pi}{2}t\,+\,2t^{2}\,+\,\frac{16}{\pi^{2} }.\]Graph II, interval (2 s; 4 s>:
The graph of the function ε(t) over this interval is: \(\varepsilon(t)\,=\,0.\)
We also know that for \(\omega(t)\) it holds that:
\[\omega(t)\,=\,\int{\epsilon(t)}dt,\] \[\omega(t) \,=\,\int{0}dt \,=\, C.\]We know the equation for \(\omega(t)\) over the interval <0 s; 2 s>, so we can calculate the value of \(\omega(2)\) at time 2 s:
\[\omega(2)\,=\,\frac{8}{\pi}\sin\frac{\pi}{2}2\,+\,4{\cdot} 2\,=\,8.\]We can calculate the constant C from the initial conditions:
\[t\,=\,2\,\mathrm{s}, \hspace{20px} \omega(2)\,=\, 8,\] \[C\,=\,8,\]
\[\omega(t)\,=\,8.\]For \(\alpha(t)\) it holds that:
\[\alpha(t)\,=\,\int{\omega(t)}dt,\] \[\alpha(t)\,=\,\int{8}dt\,=\,8t\,+\,C.\]We know the equation for \(\alpha(t)\) over the interval <0 s; 2 s>, so we can calculate the value of \(\alpha(2)\) at time 2 s:
\[\alpha(2)\,=\,-\frac{16}{\pi^{2}}\cos\frac{\pi}{2}2\,+\,2{\cdot} 2^{2}+\frac{16}{\pi^{2}}\,=\,\frac{32}{\pi^{2}}\,+\,8.\]We can calculate the constant C:
\[t\,=\,2\,\mathrm{s}, \hspace{20px} \alpha(2)\,=\,\frac{32}{\pi^{2}}+8,\] \[\frac{32}{\pi^{2}}\,+\,8\,=\,8{\cdot} 2\,+\,C\,=\,16\,+\,C,\] \[C\,=\,\frac{32}{\pi^{2}}-8,\]
\[\alpha(t)\,=\,8t\,+\,\frac{32}{\pi^{2}}-8.\]ANSWER
Graph I, interval <0 s; 2 s>:
\[\varepsilon\,=\,2t^{2},\] \[\omega(t)\,=\,\frac{2}{3}t^3,\] \[\alpha(t)\,=\,\frac{t^{4}}{6}.\]Graph I, interval (2 s; 4 s>:
\[\varepsilon(t)\,=\,8,\] \[\omega(t)\,=\,8t\,-\,\frac{32}{3},\] \[\alpha(t)\,=\,4t^{2}\,-\,\frac{32}{3}t\,+\,8.\]Graph II, interval <0 s; 2 s>:
\[\varepsilon(t)\,=\,4\cos\frac{\pi}{2}t\,+\,4,\] \[\omega(t)\,=\,\frac{8}{\pi}\sin\frac{\pi}{2}t\,+\,4t,\] \[\alpha(t)\,=\,-\frac{16}{\pi^{2} }\cos\frac{\pi}{2}t\,+\,2t^{2}\,+\,\frac{16}{\pi^{2} }.\]Graph II, interval (2 s; 4 s>:
\[\varepsilon(t)\,=\,0,\] \[\omega(t)\,=\,8,\] \[\alpha(t)\,=\,8t\,+\,\frac{32}{\pi^{2}}-8.\]