Collection of Solved Problems in Physics

Steel ball

Task number: 2226

• List of known information

  a = 0,5 m·s−2	ball’s acceleration
  s =  20 m	total travelled distance
  t = 12 s	total time of balls movement
  t1 = ? (s)	time of ball’s movement on the angled plane

• Hint 1: Distance and speed of ball on angled plane

  Draw a picture and mark all needed quantities.

  What distance will the ball travel on the angled plane and what speed will it reach?

• Solution to Hint 1

  Picture:

  

  The ball moves on the angled plane with a uniformly accelerated straightforward motion. Then, on the flat plane, it moves with a uniform straightforward motion. On the angled plane, the ball moves for t₁ with a set acceleration a. In this time it travels the distance of:

  \[s_1\,=\,\frac{1}{2}\,at_1^{2}\,,\]

  and reaches the speed of

  \[v\,=\,at_1\,.\]

• Hint 2: Ball’s movement on level plane

  What is the ball’s movement on the level plane?

  What is its speed during this movement?

  What distance does it travel?

• Solution to Hint 2

  The ball moves with even straightforward motion on the level plane.

  It moves with the speed of v which it reached on the angled plane.

  It moves with this speed on the level plane for time of t − t₁ and is travels the distance of s₂:

  \[s_2\,=\,v(t\,-\,t_1)\,=\,at_1(t-t_1)\,.\]

• Hint 3: Total distance of the ball

  Express the total distance the ball has travelled.

  Solve the quadratic equation that you get for time t₁ and figure out which root of the equation fits the task’s conditions.

• Solution to Hint 3

  The total distance will be:

  \[s\,=\,\frac{1}{2}\,at_1^{2}\,+\,at_1\left(t\,-\,t_1\right)\,.\]

  We multiply the brackets:

  \[s\,=\,-\frac{1}{2}\,at_1^{2}\,+\,at_1t\,.\]

  And after adjusting:

  \[t_1^{2}\,-\,2tt_1\,+\,\frac{2s}{a}\,=\,0\,.\]

  By solving the quadratic equation, we get two roots (marked as t₁, t₂); only one fits:

  \[t_1\,=\,t\,-\,\sqrt{t^{2}\,-\,\frac{2s}{a}}\,.\]

  Because:

  \[t_1\,<\,t\,.\]

  Numerically:

  \[t_1\,=\,\left(12\,-\,\sqrt{(12)^{2}\,-\,\frac{2{\cdot} 20}{0{,}5}}\right) \,\mathrm{s} \,=\, 4\,\mathrm{s}\,.\]

• Overall Solution

  Picture and marking of quantities:

  

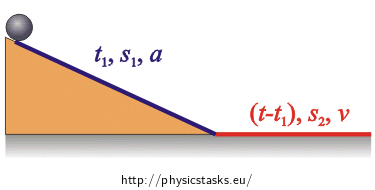
  The ball moves on the angled plane with a uniformly accelerated straightforward motion. Then, on the level plane, it moves with a uniform straightforward motion. On the angled plane, the ball moves for t₁ with a set acceleration a. In this time it travels the distance of:

  \[s_1\,=\,\frac{1}{2}at_1^{2}\,.\]

  And will reach the speed:

  \[v\,=\,at_1\,.\]

  It will move on the level plane with this speed for time of t - t₁ and will travel the distance:

  \[s_2\,=\,v\left(t-t_1\right)\,=\,at_1\left(t-t_1\right)\,.\]

  Total distance will be:

  \[s\,=\,\frac{1}{2}\,at_1^{2}\,+\,at_1\left(t-t_1\right)\,.\]

  We multiply the brackets:

  \[s\,=\,-\frac{1}{2}\,at_1^{2}\,+\,at_1t\,.\]

  And after adjusting:

  \[t_1^{2}\,-\,2tt_1\,+\,\frac{2s}{a}\,=\,0\,.\]

  By solving the quadratic equation, we get two roots (marked as t₁, t₂); only one fits:

  \[t_1\,=\,t\,-\,\sqrt{t^{2}\,-\,\frac{2s}{a}}\,.\]

  Because:

  \[t_1\,<\,t\,.\]

  Numerically:

  \[t_1\,=\,\left(12\,-\,\sqrt{(12)^{2}\,-\,\frac{2{\cdot} 20}{0{,}5}}\right)\,\mathrm{s}\,=\,4\,\mathrm{s}\,.\]

• Answer

  The steel ball moves on the angled plane for:

  \[t_1\,=\,t\,-\,\sqrt{t^{2}\,-\,\frac{2s}{a}}\,=\, 4\,\mathrm{s}\,.\]