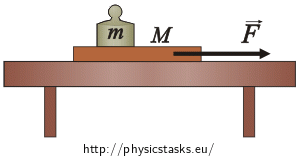
A weight on a board
Task number: 383
There is a board with mass M = 1 kg on a desk and on the board a weight with mass m = 2 kg. What is the minimal force one has to exert on the board to pull it out from under the weight? The coefficient of friction between the desk and the board is f1 = 0.35 and the coefficient of static friction between the weight and the board is f2 = 0.5.
Analysis
1. First we have to figure out what is the critical condition to pull the board out from under the weight. If we act on the board with a small force F, the weight will move together with it. What force causes the acceleration of the weight? The weight starts moving thanks to the friction force between it and the board. The magnitude of this friction equals:
\[F_{t_2}=ma\]
2. Increasing the force pulling the board increases the acceleration of it, too. In order to start the weight moving, friction has to act on it. The maximum value of static friction is:
\[F_{t_2max}=mgf_2\]
If we act on the board in such a way (with such a force F) that the acceleration of the board is bigger than the maximum acceleration of the weight that can be supplied by the static friction, we will pull out the board from under the weight. For the maximum acceleration we can impart to the board so that the weight stays on it without moving, we can write:
\[ma_{max}=mgf_2\]
3. We know the maximum acceleration which could be imparted to the board. The desired force could now be expressed from the force equation of the board.
Hint 1 – forces acting on the board and on the weight
Draw a free body diagram of the board and the desk.
Hint 2 – force equations
Write force equations for the board and for the weight and then rewrite them as scalar equations (i.e., separate each vector equation into two equations, one for each perpendicular component).
Hint 3 – frictions and maximum acceleration
Consider on what the magnitude of friction between the board and the desk depends and how can one express it. What is the maximum value of static friction between the weight and the board and what is the acceleration corresponding to it?
Hint 4 – calculation of force
We know the maximum value of acceleration which could be imparted to the weight and still stay on the board. From equation (7) for the board we can find out the magnitude of the pulling force which corresponds to this acceleration. If we act with a larger force than this we will pull out the board from under the weight.
COMPLETE SOLUTION
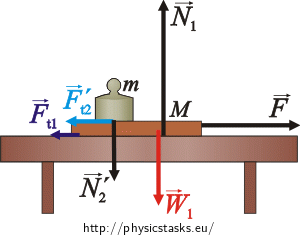
Draw a free body diagram of the board and the desk and write force equations for them.
Forces acting on the board which has mass M:
\(\vec{W}_1\)… the weight
\(\vec{N}_{1}\)… the normal force of the desk acting on the board
\(\vec{N}_{2}'\)… the normal force of the weight acting on the board
\(\vec{F}_{t_1}\)… the friction between the desk and the board
\(\vec{F}_{t_2}'\)… the friction between the board and the weight
\(\vec{F}\)… the desired force by which we pull the board
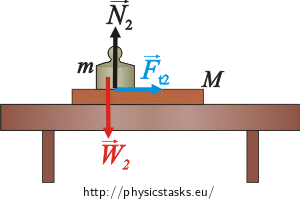
Forces acting on the weight m:
\(\vec{W}_2\)… the weight
\(\vec{N}_{2}\)… the normal force of the board acting on the weight
\(\vec{F}_{t_2}\)… the friction between the board and the weight
A force equation for the board:
\[\vec{F}_{t_1}+\vec{F}_{t_2}'+\vec{F}+\vec{W}_1+\vec{N}_1+\vec{N}_{2}'=M\vec{a}\tag{1}\]
Let’s rewrite equation (1) as two separate equations, one for each perpendicular component. Let an axis x be oriented in the direction of the motion and an axis y perpendicular to it:
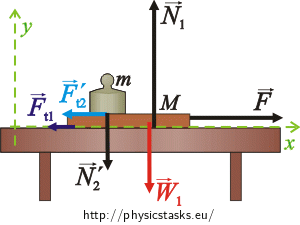
\[x:\hspace{20px}-F_{t_1}-F_{t_2}'+F=Ma\tag{2}\]
\[y:\hspace{20px}N_1-N_2'- W_1 =0\tag{3}\]
A force equation for the weight:
\[\vec{F}_{t_2}+\vec{W}_2+\vec{N}_2=m\vec{a}\tag{4}\]
Both the board and the weight move with the same acceleration.
Let’s rewrite equation (4) as two component equations; axis x should be oriented in the direction of the motion and the axis y is perpendicular to it:
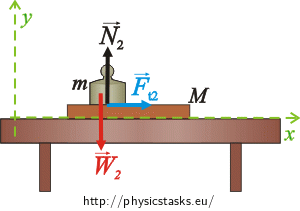
\[x:\hspace{20px}F_{t_2}=ma\tag{5}\]
\[y:\hspace{20px}N_2- W_2 =0\tag{6}\]
The board acts on the weight with force \(\vec{N}_2\) and the weight acts on the board with force \(\vec{N}_2'\). The same situation occurs with forces \(\vec{F}_{t_2}\) and \(\vec{F}_{t_2}'\). According to Newton’s third law (the law of reciprocal actions) for the magnitudes of these forces:
\[|\vec{N}_2|=|\vec{N}_{2}'|\]
\[|\vec{F}_{t_2}|=|\vec{F}_{t_2}'|\]
Equations (2) and (3) could be rewritten as:
\[-F_{t_1}-F_{t_2}+F=Ma\tag{7}\]
\[W_1-N_1+N_2=0\tag{8}\]
Frictions:
Friction \(\vec{F}_{t_1}\) acting on the board is proportional to the normal force \(\left(\vec{W}_1+\vec{N}_{2}'\right)\) by which the board acts on the desk. This force has, according to the Newton’s third law, the same value as the force \(\vec{N}_{1}\) by which the desk acts on the board. Likewise the maximum static friction \(\vec{F}_{t_2max}\) acting on the weight is proportional to the normal force \(\vec{W}_{2}\) by which the weight acts on the board. This is according to Newton’s third law the same value as the force \(\vec{N}_{2}\) by which the board acts on the weight. Let’s rewrite these thoughts in equations:
\[F_{t_1}=f_1N_1\]
\[F_{t_2max}=f_2N_2\]
Forces N1 and N2 could be expressed from equations (6) and (8) as
\[N_2=W_2\]
\[N_1=W_1+N_2=W_1+W_2\]
Frictions:
\[F_{t_1}=f_1W_1+f_1W_2=f_1Mg+f_1mg=(M+m)gf_1\]
\[F_{t_2{max}}=f_2mg\]
The maximum acceleration which could be imparted to the weight by static friction equals:
\[F_{t_2max}=mgf_2=ma_{max}\]
\[a_{max}=gf_2\tag{9}\]
Let’s put the maximum value of acceleration into equation (7):
\[F-F_{t_1}-F_{t_2}=Ma_{max}\]
Now, substitute in the explicit expressions for each friction term:
\[F-(M+m)gf_1-mgf_2=Mgf_2\]
Solve for the force F:
\[F=(M+m)gf_1+(M+m)gf_2\]
\[F=(M+m)g(f_1+f_2)\tag{10}\]
And finally, with numbers:
\[F=(1 + 2)\cdot9.81\cdot(0.35 + 0.5)\,\textrm{N}\]
\[F = 25 \,\textrm{N}\]
COMPLETE ANSWER
The minimal force one has to exert on the board to pull it out from under the weight is \(F=(M+m)g(f_1+f_2)= 25 \,\textrm{N}\).




