Moments of Inertia of a Ring and a Disc

Task number: 2234

Let us consider a thin disc and a thin ring.

A) First, try to guess without calculation, which shape, a disk or a ring, will have a greater moment of inertia if they have the same radius, mass and axis of rotation.

B) Determine the moment of inertia of a thin circular-shaped ring of mass m and radius R with respect to the axis passing perpendicularly through its centre.

C) Determine the moment of inertia of a thin circular disk of radius R and mass m with respect to the axis passing perpendicularly through its centre.

Hint A
Think about the quantities on which moment of inertia of a body depends.
Solution of Hint A
Moment of inertia depends on the mass distribution with respect to the axis of rotation. It increases with a second power of distance from the axis. Thus, if the disk and ring have the same mass, then the ring has a greater moment of inertia because its entire mass is concentrated in its perimeter (we could say it is not “full”).
Hint 1B
Review the theory explained in the task Moment setrvačnosti tyče. How can we use it in this task?
Solution of Hint 1B
First, we can solve the task by a simple consideration. Imagine that we cut the ring into small pieces of length ds and mass dm. All these “pieces” are equidistant from the axis of rotation (distance R) and the moment of inertia of each piece is equal to:
\[ dJ_r = dmR^2\,.\]
(based on the formula for the moment of inertia of a mass point). Then, by adding together the moments of inertia of all pieces, we obtain the total moment of inertia. So, the result is:
\[J_r = dm_1R^2 + dm_2R^2 + dm_3R^2 + ... =R^2(dm_1 + dm_2 + dm_3 + ...) = mR^2\,.\]
We can also verify this result by calculation.

A thin circular ring can be considered as an object characterized only by its length. So we adjust the general relation using volume integral:

\(J = \int_{V} \rho R^2 dV\)→ \(J_r = \int \lambda R^2 ds,\)

where the limits of the integral are the start and end points of the curve, λ is the linear mass density and ds length of an infinitesimally small part of the curve.
Hint 2B
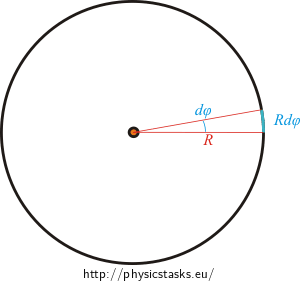
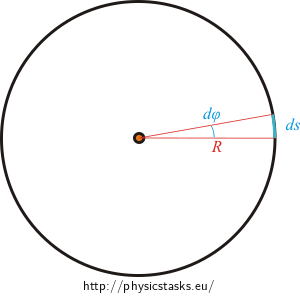
Think about the shape of the integral. Knowing the radius of the circle, how do we express the length of a small piece of the curve ds if we consider that it corresponds with an infinitely small angle dφ? Does this perspective make the determination of the limits of the integral easier?
Solution of Hint 2B
If we determine the angle in an arc length measure (i.e. in radians), then its magnitude is
\[\varphi = \frac{s}{R}\,,\]
where s is the length of the cut-out circular arc and r radius of the circle.

Then, for an infinitely small arc it holds true:
\[ds = Rd\varphi\,. \]

So, we integrate using the angle. Since the ring has a circular shape, limits of the integral are 0 and 2π (i.e. integral over the entire circle).
\[J_r = \int \lambda R^2 ds\,,\] \[J_r = \int^{2\pi}_{0} \lambda R^2 Rd\varphi\,,\] \[J_r = \int^{2\pi}_{0} \lambda R^3 d\varphi = \lambda R^3\left[\varphi\right]_{0}^{2\pi} = \lambda R^3 2\pi\,.\]
Let us recall the formula for the linear mass density of a circle:
\[\lambda = \frac{m}{C} = \frac{m}{2\pi R}\,,\] \[m = 2\pi\lambda R\,.\]
And therefrom:
\[J_r = mR^2\,.\]
Hint 1C
What is the difference in calculation of the moment of inertia of a disk and a ring? Will the results from the previous section be useful to us?
Solution of Hint 1C
A disk could be viewed as a body formed by an infinite number of thin rings, which gradually fill the entire radius, added together.

Try to change the consideration from the previous question in the spirit of this approximation.
Hint 2C
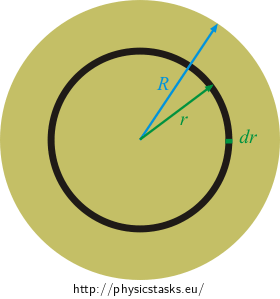
Express the moment of inertia of one ring. Use the results from the previous section.

Then we calculate the total moment of inertia of the disk by adding up the contributions of all the rings, i.e. by integration.
Solution of Hint 2C
Moment of inertia of one ring is:
\[dJ_d = dmr^2\,\] ,
where r is the radius and dm mass of the ring:
\[dm = \sigma 2\pi r dr\,.\]
In case of a disk, for the surface mass density σ it holds true that:
\[\sigma = \frac{m}{S} = \frac{m}{\pi R^2}\,.\]
Then:
\[dJ_d = 2\pi \sigma r^3 dr\,.\]
The total moment of inertia of the disk is obtained by adding together the moments of inertia of all rings:
\[J_d = \int dJ_d = \int_{0}^{R} 2\pi \sigma r^3 dr = 2\pi \sigma \left[\frac{r^4}{4}\right]_{0}^{R} = \frac{1}{2}\pi \sigma R^4\,.\]
Finally, we substitute the surface density:
\[J_d = \frac{1}{2}\pi\frac{m}{\pi R^2}R^4 = \frac{1}{2} mR^2\,.\]
Another possible solution of part C
The problem can also be very easily solved by the transformation into a double integral in polar coordinates:
\[J_d = \int_{S} \sigma r^2 dS\,.\]

\[dS = rd \varphi dr\,,\] \[J_d = \int_{0}^{2\pi} \int_{0}^{R} \sigma r^3 dr d \varphi = \frac{1}{2}\pi \sigma R^4 = \frac{1}{2}m R^2\,.\]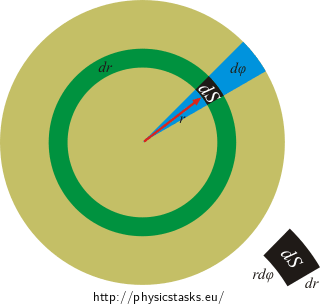
Answer
We can determine even without calculation that the moment of inertia of the ring is greater than the moment of inertia of the disk due to the mass distribution with respect to the axis of rotation.

Moment of inertia of the thin ring of mass m and radius R with respect to the axis passing through its centre is
\[J_r = mR^2\,.\]
Moment of inertia of the disk of mass m and radius R with respect to the axis passing through its centre is
\[J_d = \frac{1}{2} mR^2\,.\]