A car and a constant breaking force
Task number: 382
A car of mass m moves along a horizontal road with uniform motion and speed v0. At time t = 0 s a constant braking force FB starts acting on it. Assume that at time t = 0 s the coordinate x equals zero.
1) Determine how the velocity v(t) and the coordinate x(t) are changing with time.
2) Determine the time tsat which the car stops, and the distance xs which the car travels during stopping.

Note: Instead of a magnitude of a velocity we use just a velocity.
Hint 1 – Forces acting on a car, a motion equation
Be aware of forces acting on the car (draw a free body diagram) and write a force equation for the car.
Hint 2 – the acceleration of the car and the behaviour of v(t), x(t)
Determine the acceleration of this car, then find out the function v(t) and finally express the coordinate x as a function of time x(t).
Hint 3 – the time and the position of the stopping point
Consider what the velocity is at the moment the car stops, and use it to determine the stopping time ts. It is easy now to calculate the distance if we know the behaviour of x(t) and the stopping time ts.
Notice
The stopping distance could be also determined from the law of conservation of energy.
The initial kinetic energy of the car equals the work of the braking force acting on the stopping distance.
\[\frac{mv_0^2}{2}=F_{\textrm{B}}x_s\]
And so:
\[x_s=\frac{mv_0^2}{2F_{\textrm{B}}}\]
COMPLETE SOLUTION
Let’s draw a free body diagram of the car and write a force equation for it.
Forces acting on this car:
\(\vec{F}_{\textrm{B}}\)... the braking force
\(\vec{W}\)... the weight
\(\vec{N}\)... the normal force by which the road surface acts on the car
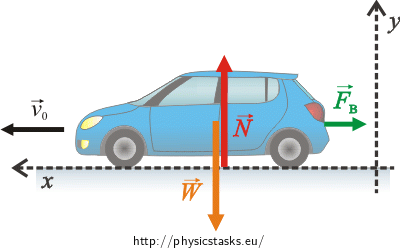
Note: The force of the surface acts on the wheels; in a free body diagram we draw their net force N.
A force equation for the car is
\[\vec{F}_{\textrm{B}}+\vec{W}+\vec{N}= m\vec{a}\tag{1}\]
We establish a coordinate system in agreement with the picture and rewrite equation (1) as two scalar equations in directions x and y.
\[x:\hspace{20px}-F_{\textrm{B}} = ma\tag{2}\]
\[y:\hspace{20px}N - W = 0\tag{3}\]
Note: From the picture one can see why there is a minus sign in equation (2). The braking force acts opposite the direction of the car’s motion. Forces \(\vec{W}\) a \(\vec{N}\) are perpendicular to the braking force \(\vec{F}_{\textrm{B}}\), they are the same magnitude and their net force is zero, so the acceleration in the y direction is also zero.
The acceleration of the car:
From equation (2) we get:
\[a =-\frac{F_{\textrm{B}}}{m}\tag{4}\]The car’s acceleration is constant and because the car decelerates, the acceleration is negative.
Behaviour of v(t):
By integration of equation (4) we get an equation for the time dependent velocity:
\[v(t)=\int{a}\,dt=\int{-\frac{F_{\textrm{B}}}{m}}\,dt=-{\frac{F_{\textrm{B}}}{m}}t+C_1\tag{5}\]
C1 is a constant which can be determined from the initial conditions:
At time t = 0 s the velocity was v = v0. If we insert t = 0 s into equation (5), we will get:
v0 = 0 + C1
And so:
v0 = C1
Rewriting equation (5) we get an equation for the time dependent velocity of the car:
\[v(t)=-{\frac{F_{B}}{m}}t+v_0\tag{6}\]
Behaviour of x(t):
By integration of equation (4) we get an equation for the time dependent velocity:
\[x(t)=\int{v(t)}\,dt=\int{(-\frac{F_{B}}{m}}t+v_0)\,dt=-{\frac{F_{B}}{2m}}t^2+v_0t+C_2\tag{7}\]
C2 is a constant which can be determined from the initial conditions:
At time t = 0 s the coordinate x = 0. If we insert t = 0 s into equation (7), we will get:
0 = 0 + C2
And so:
C2 = 0
Rewriting equation (7) we get an equation for the time dependent position of the car:
\[x(t)=-{\frac{F_{B}}{2m}}t^2+v_0t\tag{8}\]
Stopping time ts:
When the car stops the velocity equals zero. We can get the stopping time from equation (6):
\[0=-{\frac{F_{\textrm{B}}}{m}}t_s+v_0\]
Express the time ts:
\[t_s=\frac{mv_0}{F_{\textrm{B}}}\tag{9}\]
The stopping distance xs:
We obtain the position at which the car stops by inserting time ts from equation (9) into equation (8) – the dependence of the coordinate on time.
\[x_s=-{\frac{F_{\textrm{B}}}{2m}}t_s^2+v_0t_s =-{\frac{F_{\textrm{B}}}{2m}}\left(\frac{mv_0}{F_{\textrm{B}}}\right)^2+v_0\left(\frac{mv_0}{F_{\textrm{B}}}\right)\]
\[x_s=\frac{mv_0^2}{2F_{\textrm{B}}}\tag{10}\]
COMPLETE ANSWER
The equation for the time dependent velocity is \(v(t)=-{\frac{F_{\textrm{B}}}{m}}t+v_0\).
The equation for the time dependent coordinate of the car is \(x(t)=-{\frac{F_{\textrm{B}}}{2m}}t^2+v_0t\).
The stopping time of the car is \(t_s=\frac{mv_0}{F_{\textrm{B}}}\).
The stopping distance of the car is \(x_s=\frac{mv_0^2}{2F_{\textrm{B}}}\).


